円周率 π は、３．０５より大きいことを証明せよ。 | 【古典文学・法学・コンピュータ】の総合研究所

研究所トップ
ブログ
円周率 π は、３．０５より大きいことを証明せよ。

徒然日記

円周率 π は、３．０５より大きいことを証明せよ。 [徒然日記]

投稿日時：2014/10/04(土) 22:59

5年前に自己流で解いた数学の問題。

私的数学塾というサイトの掲示板に投稿した解答が紹介された。

不思議なことに、数学は忘れていないのです。

なぜこのような方法を採ったのかというと、「余弦定理」を忘れていたからです。

この解法のポイントは、

「ｓｉｎ１５°」の値が、「０．２５８８--」と記憶していたことです。

００１

平成１５年度前期

東京大学

理科系

・・・

三角関数（数学Ⅱ）

やや難

　　　　　　円周率 π は、３．０５より大きいことを証明せよ。

この問題は、多分受験生の意表を突いた問題ではなかっただろうか？今、巷間でも話題
になっている。新学習指導要領では、円周率は、３　として計算してもよいとされているが、
「円周率は、やっぱり　３　より大きいよね！」という東大からのメッセージではないかとい
う穿った見方もできる。

　円周率 π ＝３．１４１５９・・・　という知識しかない場合は、全くのお手上げ状態だったろ
うと推察される。昔、慶應義塾大学で、対数の定義を問う問題が出題されたが、教科書レ
ベルの内容にも関わらず、不意をつかれた受験生は戸惑ったらしい。

（追記）　平成２０年１０月１５日付け

　　　　　当ＨＰの掲示板「出会いの泉」に、１４日付けで、ＨＮ「カズ」さんが次のように書き込
　　　　まれた。（多少文言等を修正させていただきました。）

　　　　　　　先日、高1の末娘が通う塾の2年次説明会で、上記の東大入試問題のことを
　　　　　　聞いた。三角関数の基本事項だけで証明して、娘に教えてやろうとの想いで、
　　　　　　自己流で証明をしてみた。

　　　　　　（証明方法）

　　　　　　(1)　半径が 1 の円Ａに内接する正十二角形の12等分された1つの△ＡＢＣを考
　　　　　　　　える。このとき、円弧ＢＣ＝π/6で、π＞６×ＢＣ　が成り立つ。

　　　　　　(2)　次に、ＢＣ×1/2＝ｓｉｎ１５°より、ＢＣ＝２×ｓｉｎ１５°となるので、(1)より、
　　　　　　　　π＞１２×ｓｉｎ１５°となる。

　　　　　　(3)　このとき、ｓｉｎ１５°＞０．２５８８から

　　　　　　　　π＞１２×ｓｉｎ１５°＞１２×０．２５８８＝３．１０５６＞３．０５　となる。

　　　　　　(4)　したがって、円周率 π は、３．０５より大きい。

　　　　　　この証明方法は、「余弦定理」・「加法定理」等を使用していないこと、ｓｉｎ１５°
　　　　　の近似値を用いたことにより、計算も単純で、非常に理解しやすいと思う。

（コメント）　上記の「カズ」さんの証明は、基本的に再追記で述べた面積利用の証明と
　　　　　　　　　一致する。

　　　　　　　　　　ｓｉｎ１５°の値を（再追記）では加法定理を用いて求めたが、次の図形から
　　　　　　　　　も求められる。

　　　　　　　　　　　　　　　　　

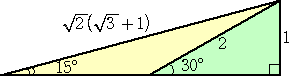
　　　　　　　　　上図の斜辺の計算には、二重根号を外す計算（教科書では発展レベル）が
　　　　　　　　必須である。この点を除外すれば、「カズ」さんの証明は十分高校１年レベル
　　　　　　　　と言える。証明を頂いた「カズ」さんに感謝します。

　　　　　　　　　（追記）　平成２０年１１月３日付け

　　　　　　　　　　　上図を用いて、ｓｉｎ１５°の値を計算する場合、二重根号の計算は避け
　　　　　　　　　　られないが、下図を用いると、二重根号の計算が回避できて、ｓｉｎ１５°
　　　　　　　　　　の値が求められることを、カズさんからご教示いただいた。

　　　　　　　　　　　Ｂ＝３０°、Ｃ＝９０°の直角三角形ＡＢＣにおいて、辺ＢＣ上に、

　　　　　　　　　　∠ＡＤＣ＝４５°となる点Ｄをとり、点Ｄより辺ＡＢに垂線ＡＨを引く。

　　　　　　　　　　このとき、∠ＤＡＨ＝１５°である。

　　　　　　　　　　　　　　　　　　

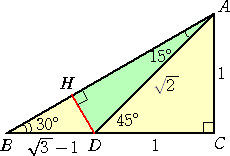
　　　　　　　　　　　　　上図において、　ＤＨ＝（－１）/２　なので、

　　　　　　　　　　　　　　　　ｓｉｎ１５°＝（－１）/２＝（－）/４

　　　　　　　　　　　　と求められる。

　　　　　　　　　　　　（コメント）　簡明に求められる図に感動しました。カズさんに感謝いた
　　　　　　　　　　　　　　　　　　します。