徒然日記 2014/10/4
円周率 π は、3.05 より大きいことを証明せよ。
[徒然日記] 投稿日時:2014/10/04(土) 22:59
5年前に自己流で解いた数学の問題。
私的数学塾というサイトの掲示板に投稿した解答が紹介された。
不思議なことに、数学は忘れていないのです。
なぜこのような方法を採ったのかというと、「余弦定理」を忘れていたからです。
この解法のポイントは、
「sin15°」の値が、「0.2588--」と記憶していたことです。
|
001 |
平成15年度前期 | 東京大学 | 理科系 | ・・・ | 三角関数(数学Ⅱ) | やや難 |
円周率 π は、3.05 より大きいことを証明せよ。
この問題は、多分受験生の意表を突いた問題ではなかっただろうか?今、巷間でも話題
になっている。新学習指導要領では、円周率は、3 として計算してもよいとされているが、
「円周率は、やっぱり 3 より大きいよね!」という東大からのメッセージではないかとい
う穿った見方もできる。
円周率 π =3.14159・・・ という知識しかない場合は、全くのお手上げ状態だったろ
うと推察される。昔、慶應義塾大学で、対数の定義を問う問題が出題されたが、教科書レ
ベルの内容にも関わらず、不意をつかれた受験生は戸惑ったらしい。
(追記) 平成20年10月15日付け
当HPの掲示板「出会いの泉」に、14日付けで、HN「カズ」さんが次のように書き込
まれた。(多少文言等を修正させていただきました。)
先日、高1の末娘が通う塾の2年次説明会で、上記の東大入試問題のことを
聞いた。三角関数の基本事項だけで証明して、娘に教えてやろうとの想いで、
自己流で証明をしてみた。
(証明方法)
(1) 半径が 1 の円Aに内接する正十二角形の12等分された1つの△ABCを考
える。このとき、円弧BC=π/6で、π>6×BC が成り立つ。
(2) 次に、BC×1/2=sin15°より、BC=2×sin15°となるので、(1)より、
π>12×sin15°となる。
(3) このとき、sin15°>0.2588 から
π>12×sin15°>12×0.2588=3.1056>3.05 となる。
(4) したがって、円周率 π は、3.05 より大きい。
この証明方法は、「余弦定理」・「加法定理」等を使用していないこと、sin15°
の近似値を用いたことにより、計算も単純で、非常に理解しやすいと思う。
(コメント) 上記の「カズ」さんの証明は、基本的に再追記で述べた面積利用の証明と
一致する。
sin15°の値を(再追記)では加法定理を用いて求めたが、次の図形から
も求められる。
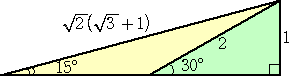
上図の斜辺の計算には、二重根号を外す計算(教科書では発展レベル)が
必須である。この点を除外すれば、「カズ」さんの証明は十分高校1年レベル
と言える。証明を頂いた「カズ」さんに感謝します。
(追記) 平成20年11月3日付け
上図を用いて、sin15°の値を計算する場合、二重根号の計算は避け
られないが、下図を用いると、二重根号の計算が回避できて、sin15°
の値が求められることを、カズさんからご教示いただいた。
B=30°、C=90°の直角三角形ABCにおいて、辺BC上に、
∠ADC=45°となる点Dをとり、点Dより辺ABに垂線AHを引く。
このとき、∠DAH=15°である。
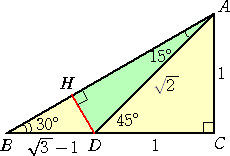
上図において、 DH=(![]() -1)/2 なので、
-1)/2 なので、
sin15°=(![]() -1)/2
-1)/2![]() =(
=(![]() -
-![]() )/4
)/4
と求められる。
(コメント) 簡明に求められる図に感動しました。カズさんに感謝いた
します。
※私的数学塾より引用しています。
当該URL
本問のページ
http://shochandas.xsrv.jp/inquiry/inquiry001.htm
2014年10月
| <<前月 | 翌月>> |
| |
| |
| |
 ログイン
ログイン