【古典文学・法学・コンピュータ】の総合研究所

「なぜ『古事記』の研究なのか？」を、あるサイトに投稿した。

以下、投稿内容の記録です。

『古事記』に夢中の毎日です。　  2014.10. 4に投稿

　2014年4月1日から、私の「第二の人生」がスタートした。職場を退職する前に、ライフワークとして『古事記』の研究をすることを決めていたので、再任用の途を閉ざし「自由な時間と生活」を手に入れた。
　退職前から現在に至るまで「なぜ『古事記』の研究なの？」と、多くの友人・知人から聞かれた。この問いかけに答えるために、本稿を書いてみる。
 

※「母との別れが私のライフワークを決めた」
　2012年2月25日、母が他界した。満93歳であった。母との永遠の別れは、私の人生の中で最大の悲しい出来事だった。しかし母を荼毘に付した後、悲しい気持ちは消え「母から解放された。これからは自分の人生だ。好きなように生きたい」と思ったのである。
　私がこのように思ったのは、満8歳の時に父と死別し幼心に「これからは母を支えていこう」と心に決めこの五十年間を生きてきたからである。母は父と死別した後、残された三人の子供を女手一つで苦労して育てた人である。だから私は常に「母への感謝と尊敬の気持ち」を持ち続け、母が最優先で自分は二番手との生き方をしてきた。このことで妻からはよく小言を言われたが「幼心で決めたこと」を最後まで貫徹したのである。
　母と別れた後、初めて自分の人生について真剣に考えることになった。その結論は「これからは自分が最優先。夢を持って、自由奔放に生きること」であった。そして、「自分は何がしたかったのか」と自問自答した結果、「古事記の研究」がしたかったことが蘇ってきた。
そんな訳で、自分のライフワークは『古事記』の研究と決めた。将来の夢は大学院に行き『古事記』の研究を完成させことである。しかし高卒のままでは大学院進学は困難であり、やむなく2012年春に通信制大学に入学した。大学卒業資格を得るための４年間は、『古事記』の研究にとって、もったいない時間である。本当は、その時間を全部『古事記』の研究に費やしたいところだが、大卒資格を取らないと次のステップに到達しないのである。頑張るしかない。

※「なぜ『古事記』の研究なのか？」
　私が『古事記』のどこに魅かれたのか。それは、ズバリ「上巻の冒頭で神が成る」との表現である。つまり、「無から有が生じる」との哲学的な文章に魅かれたのである。
『古事記』の上巻の冒頭は、次のように記載されている。
【原文】
「天地初發之時、於高天原成神名、天之御中主神。次高御産巣日神。次神産巣日神。此三柱神者、並獨神成坐而、隱身也。------------」
【読み下し文】
「あめつちのはじめのとき、たかあまはらになりませるかみのみなは、アメノミナカヌシノカミ。つぎにタカミムスヒノカミ。つぎにカミムスヒノカミ。このみはしらのかみはみな、ひとりがみなりまして、みみをかくしたまひき。------------」
【現代語訳】
「天と地が初めてひらけた時に、高天原に出現した神の名は、アメノミナカヌシノカミ。次にタカミムスヒノカミ。次にカミムスヒノカミ。この三柱の神は、それぞれ一神としての単独神であり、その姿を隠されたのである。------------」
　この後も、どんどん「神」が成り続け、最後に「イザナギノカミ・イザナミノカミ」の二柱の神が成り一段落するのである。ただし「無から有が生じる」のは、ここまでである。
　私が『古事記』に魅かれたのは以上のような単純な理由であるが、『古事記』を読み解いていくと非常に面白くて夢中になってしまう。とりわけ、上巻の「黄泉の国譚」、「天の岩屋戸譚」、「八岐大蛇退治譚」などは、いつも私の頭の中を駆け巡っている。
私の研究テーマは、『古事記』の上巻(神代編)の「出雲神話」である。具体的には、スサノオの「オロチ退治」から、オオクニヌシの「国造り」、そして「国譲り」までの部分である。また、『古事記』は、序文の偽書説、本文の偽書説、「歴史書」とする説、『日本書紀』の優位説等々、古より様々な論議がされている。しかし、それらの論議には加わらず、『古事記』を「漢字テキスト」の古代文学として読み解きたいと考えている。

※「退職後、半年が経過した」
　私の「第二の人生」がスタートしてから、あっという間に半年が経過した。「サンデー毎日」の生活にも少しは慣れてきたところである。毎日、好きなだけ寝ることができるし、本も好きなだけ読める。まさに、自分があこがれていた生活である。ただ、不満は、収入が激減したことである。まあ「自由な生活」との引き換えだから仕方がないと自分に言い聞かせている。
　退職後の課題として、「古事記の研究」と「法律研究(主に民法の家族法)」と「コンピュータ研究」と決めていた。『古事記』の研究だけでは「現実逃避」に近い生き方となってしまうからだ。だから、社会の動きと変化に機敏に反応できる自分でありたいと考えている。

　以上、ダラダラと駄文を書いてきた。まとまりのない投稿文で、恥ずかしい限りです。ご容赦願います。最後に、私の「2014年5月23日のブログ記事」を紹介して投稿とします。

---------------------------ブログの記事の紹介---------------------------

ブログ投稿日時：2014/05/23(金)
表題「今年の4月から、水曜日と金曜日の2回、関学へ聴講に通っています。」

　今日は、『日本書誌学』の講義日。主として江戸期の『和本』に関する講義です。この講義では、所謂「変体仮名」についても簡単なものが読めるようになると思います。
　金曜日の講義には、末娘(関学4回生)も一緒に履修しており、父娘が『講義室で机を並べて講義を聞く』という、ちょっと珍しい事態が発生しています。しかしながら、毎週金曜日は、昼食とか、お茶代とか、本代とか、色々と払わされるので無収入の身には辛いものがある。
　水曜日は、一人で、『日本文学特殊講義』に通っています。こちらのほうは、「江戸・明治の漢文・漢詩」の講義です。今週は、日本独自の「漢文訓読＝漢語」が、現在の日本語文脈を作ってきたことについての講義でした。この講義は、非常に興味深く聞いており、38歳講師の博学ぶりには、毎回驚かされます。よく研究されておられます。講義の中身は「まとめ」をし、別のブログ(古典文学)で紹介します。
　今期は、たまたま「江戸」というキーワードで「江戸文学・文化・歴史」に触れることとなったが、「江戸」は本当におもしろい時代であると考えました。

---------------------------ブログの記事の紹介---------------------------

※掲載の写真は、以下から引用させていただきました。
記事名称「ヤマタノオロチ伝説を巡る旅 in 雲南市」
http://tegost.net/hinoborinosato/kayabuki.php?pagetag=3

 

5年前に自己流で解いた数学の問題。

私的数学塾というサイトの掲示板に投稿した解答が紹介された。

不思議なことに、数学は忘れていないのです。

なぜこのような方法を採ったのかというと、「余弦定理」を忘れていたからです。

この解法のポイントは、

「ｓｉｎ１５°」の値が、「０．２５８８--」と記憶していたことです。 

　　　　　　円周率 π は、３．０５ より大きいことを証明せよ。

この問題は、多分受験生の意表を突いた問題ではなかっただろうか？今、巷間でも話題
になっている。新学習指導要領では、円周率は、３　として計算してもよいとされているが、
「円周率は、やっぱり　３　より大きいよね！」という東大からのメッセージではないかとい
う穿った見方もできる。

　円周率 π ＝３．１４１５９・・・　という知識しかない場合は、全くのお手上げ状態だったろ
うと推察される。昔、慶應義塾大学で、対数の定義を問う問題が出題されたが、教科書レ
ベルの内容にも関わらず、不意をつかれた受験生は戸惑ったらしい。

（追記）　平成２０年１０月１５日付け

　　　　　当ＨＰの掲示板「出会いの泉」に、１４日付けで、ＨＮ「カズ」さんが次のように書き込
　　　　まれた。（多少文言等を修正させていただきました。）

　　　　　　　先日、高1の末娘が通う塾の2年次説明会で、上記の東大入試問題のことを
　　　　　　聞いた。三角関数の基本事項だけで証明して、娘に教えてやろうとの想いで、
　　　　　　自己流で証明をしてみた。

　　　　　　（証明方法）

　　　　　　(1)　半径が 1 の円Ａに内接する正十二角形の12等分された1つの△ＡＢＣを考
　　　　　　　　える。このとき、円弧ＢＣ＝π/6で、π＞６×ＢＣ　が成り立つ。

　　　　　　(2)　次に、ＢＣ×1/2＝ｓｉｎ１５°より、ＢＣ＝２×ｓｉｎ１５°となるので、(1)より、
　　　　　　　　π＞１２×ｓｉｎ１５°となる。

　　　　　　(3)　このとき、ｓｉｎ１５°＞０．２５８８ から

　　　　　　　　π＞１２×ｓｉｎ１５°＞１２×０．２５８８＝３．１０５６＞３．０５　となる。

　　　　　　(4)　したがって、円周率 π は、３．０５ より大きい。

　　　　　　この証明方法は、「余弦定理」・「加法定理」等を使用していないこと、ｓｉｎ１５°
　　　　　の近似値を用いたことにより、計算も単純で、非常に理解しやすいと思う。

（コメント）　上記の「カズ」さんの証明は、基本的に再追記で述べた面積利用の証明と
　　　　　　　　　一致する。

　　　　　　　　　　ｓｉｎ１５°の値を（再追記）では加法定理を用いて求めたが、次の図形から
　　　　　　　　　も求められる。

　　　　　　　　　　　　　　　　　

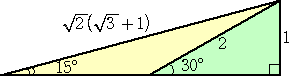
　　　　　　　　　上図の斜辺の計算には、二重根号を外す計算（教科書では発展レベル）が
　　　　　　　　必須である。この点を除外すれば、「カズ」さんの証明は十分高校１年レベル
　　　　　　　　と言える。証明を頂いた「カズ」さんに感謝します。

　　　　　　　　　（追記）　平成２０年１１月３日付け

　　　　　　　　　　　上図を用いて、ｓｉｎ１５°の値を計算する場合、二重根号の計算は避け
　　　　　　　　　　られないが、下図を用いると、二重根号の計算が回避できて、ｓｉｎ１５°
　　　　　　　　　　の値が求められることを、カズさんからご教示いただいた。

　　　　　　　　　　　Ｂ＝３０°、Ｃ＝９０°の直角三角形ＡＢＣにおいて、辺ＢＣ上に、

　　　　　　　　　　∠ＡＤＣ＝４５°となる点Ｄをとり、点Ｄより辺ＡＢに垂線ＡＨを引く。

　　　　　　　　　　このとき、∠ＤＡＨ＝１５°である。

　　　　　　　　　　　　　　　　　　

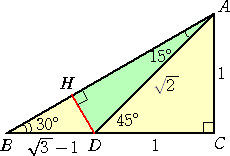
　　　　　　　　　　　　　上図において、　ＤＨ＝（－１）/２　なので、

　　　　　　　　　　　　　　　　ｓｉｎ１５°＝（－１）/２＝（－）/４

　　　　　　　　　　　　と求められる。

　　　　　　　　　　　　（コメント）　簡明に求められる図に感動しました。カズさんに感謝いた
　　　　　　　　　　　　　　　　　　します。
 

※私的数学塾より引用しています。

当該URL

http://shochandas.xsrv.jp/

本問のページ

http://shochandas.xsrv.jp/inquiry/inquiry001.htm

だんだんと秋が深まってきました。

今日から10月です。

9月は、名古屋、大阪、博多、熊本と神戸を離れる日が多かった。

10月こそは、勉学に励もうと考えています。

その1　※懸賞論文を書くこと　テーマ「民法772条の限界と父子関係のあり方」

その2　※古事記の講義録の検討　「パワーポイント原稿」

その3　※通信科目のレポート提出　「語学2科目(英語・中国語)、その他2科目」の最低4科目と試験の準備

以上の予定です。とりわけ、遅れている通信科目のレポート提出を優先しなければ。

また、関学文学部の聴講は、毎週火曜日です。

だから、10月からは、多忙な日々が続きます。ガンバロウ。